1.寄存器分配概述
寄存器是位于CPU或GPU内部的少量的高速存储器,用于保存机器指令的操作数。由于其价格昂贵导致其数量有限,又由于存取速度快,使其不可或缺。因此,寄存器是计算机体系结构中的关键资源之一。在计算复杂表达式的过程中产生的中间结果也保存在寄存器中。更复杂的编译器会把经常使用的变量放在寄存器里,来避免反复地存取。如果是优化的编译器,会把公共子表达式消除或者循环不变量移动以后的重用值放在寄存器中。
在编写高级语言程序时会用到变量,如int x、string y等。大部分程序不关心变量在计算机体系结构中用什么形式表示。从程序开发者的角度看,变量中的数据通常被认为保存在内存中,可以通过文件I/O接口在硬盘和内存之间转移,而编译器负责在内存和寄存器之间转移数据,以便CPU或GPU可以操作寄存器中的数据。从存储结构的角度看,硬盘、内存、缓存(cache)和寄存器特点不同,总结如下:
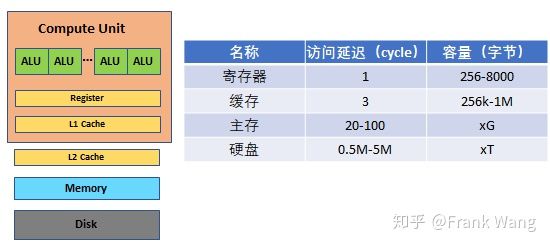
在编译的代码生成阶段,程序中的变量会被编译器替换为寄存器。高级语言程序中使用的变量数量可以是几乎无限的,但CPU或GPU中的寄存器数量是有限的,寄存器分配器作为后端的一个模块要解决这对矛盾,控制寄存器的分配和使用。因此,寄存器分配是将程序中的数量无限的虚拟寄存器映射到数量有限的物理寄存器。不同的目标设备有不同数量的物理寄存器。如果物理寄存器的数量不足以满足虚拟寄存器的需求,有些虚拟寄存器显然就只能映射到内存。这些虚拟寄存器称为溢出(spill)虚拟寄存器。寄存器分配算法的好坏直接决定了程序中寄存器的利用率。
寄存器分配可以工作在表达式、基本块、函数(也称全局)或整个程序级别。为了支持全局的优化,必须实现全局寄存器分配。历史上出现过的寄存器分配算法有:图着色算法、线性扫描算法、整数线性规划算法、PBQP算法、Multi-Flow Commodities算法、基于SSA的寄存器分配。LLVM没有全部支持上述寄存器分配算法,LLVM中支持的寄存器分配算法有4种:Basic Register Allocator、Fast Register Allocator、PBQP Register Allocator、Greedy Register Allocator。
在LLVM中,物理寄存器由范围从1到1023的整型数标识。具体目标设备的物理寄存器编号可以从中对应的
本文先介绍寄存器分配算法,然后介绍如何在LLVM中实现寄存器分配。
2. 图着色问题
寄存器分配可以抽象成图着色问题,下面先介绍什么是图着色。
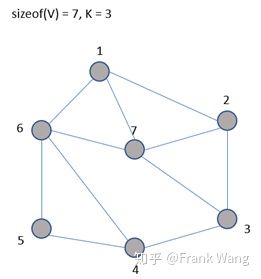
给定一个无向连通图G=(V, E),其中V为顶点集合{1, 2, …, n},E为边集合。图着色问题即为用K种颜色为图的顶点着色,每个顶点着一种颜色。要求G的每条边相连的两个顶点着不同颜色。
以下图为例,图中顶点数为7,颜色数为3。
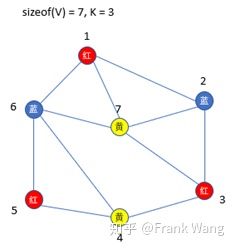
下图是其中的一种着色方案,图中的每个顶点被着以不同的颜色,同一条边两端的顶点颜色不同。
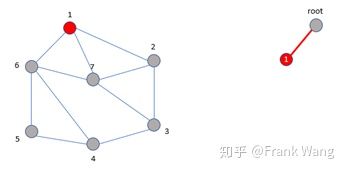
图着色算法一般采用m叉搜索树,搜索策略采用深度优先。约束条件是在节点<x1,x2, … ,xk>处,顶点k+1的邻接表中节点已经用过的颜色不能再用;如果邻接表中节点已用过m种颜色,则节点k+1没法着色,从该节点回溯到其父节点。
从root节点出发,先给节点1着红色。
接下来对节点2不能再用红色(红色虚线表示不能使用红色着色),因为节点1、2是同一条边的两个顶点。因此节点2可以用其它颜色,如蓝色。
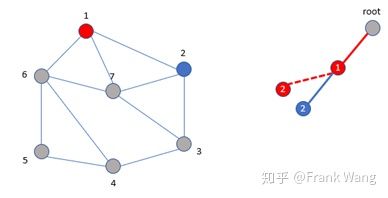
此后对节点3还可以用红色,但是对节点4不能用红色。原因同上。因此,节点4用蓝色。同理,节点5用红色。
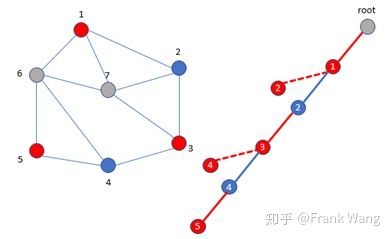
但是对节点6不能再用红色和蓝色,因为节点6与节点1、4、5都关联,无论用红色或蓝色都会与其它节点冲突。因此节点6只能另选颜色,如黄色。
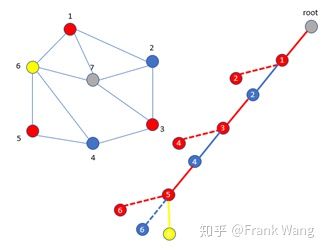
对节点7不能再用红色、蓝色和黄色,因为节点7与节点1、2、3、6都关联,无论用红色、蓝色或黄色都会与其它节点冲突。因为本例中限制颜色数量为3,因此节点7无法再着色。
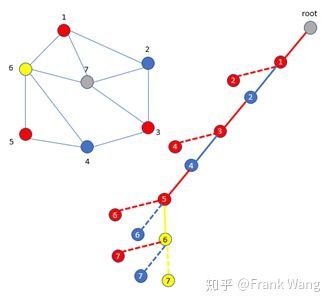
为了对节点7着色,回溯到其父节点6、5,仍没有可行解,进一步回到节点4。此时再对节点5着色,但不能用蓝色,只能考虑黄色。
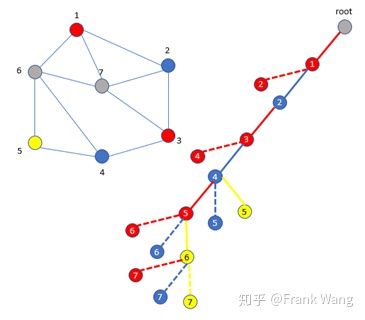
此时对接下来的节点6仍没有可行解,只能再回溯到父节点3。
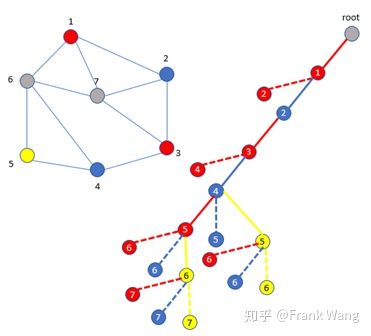
此时对节点4只能用黄色。然后节点5用红色,对节点6用蓝色,对节点7用黄色。最终得到可行解。
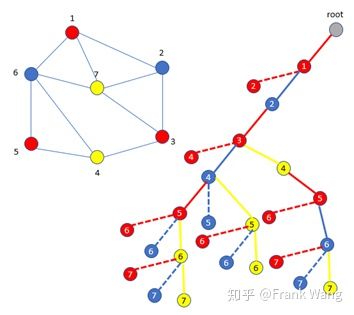
3. 图着色寄存器分配
如果寄存器分配问题被抽象成图着色问题,那么图中的每个节点代表某个变量的活跃期或生存期(Live range)。活跃期定义是从变量第一次被定义(赋值)开始,到它下一次被赋值前的最后一次被使用为止。两个节点之间的边表示这两个变量活跃期因为生命期(lifetime)重叠导致互相冲突或干涉。一般说来,如果两个变量在函数的某一点是同时活跃(live)的,它们就相互冲突,不能占有同一个寄存器。
假设有如下代码:
int a, b, c, d, e, f;
a = c – d;
e = a – b;
f = e + 3;在表达式“e = a – b;”之后,变量a就没有被再使用。同样,在表达式“f = e + 3;”之后,变量e就没有被再使用。因此,a、e、f可以被分配给同一个寄存器而寄存器中保存的值不会产生冲突。
经过上述处理,可以只使用4个寄存器s1、s2、s3、s4替换6个变量,代码可表示为:
s1 = s2 - s3
s1 = s1 - s4
s1 = s1 + 3那么,如何做到将一个寄存器分配给多个变量又不至引起冲突呢?可以遵循以下5个步骤:
步骤1:画出控制流图(CFG)
步骤2:执行活跃分析(Liveness analysis)
步骤3:画出寄存器干涉图
步骤4:执行图着色
步骤5:基于着色图分配寄存器
控制流图是以基本块为结点的有向图G=(N,E),其中N是结点集合,表示程序中的基本块;E是边的集合。如果从块U的出口转向块V,则从U到V有一条有向边U->V,表示从结点U到V存在一条可执行路径。称U为V的前驱结点,V为U的后继结点。也就代表在执行完结点U中的代码语句后,有可能顺序执行结点V中的代码语句。
假设有如下代码:
L1: a = b + c;
d -= a;
e = d + f;
if (e > 0)
f = 2*e;
else {
b = d + e;
e = e – 1;
}
b = f + c;
goto L1;上述代码的控制流图如下:
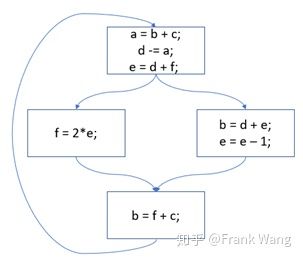
控制流图中的每一个节点代表一个程序基本块,节点之间的边代表基本块之间的控制转移。
根据图着色方法为以上代码分配寄存器,首先要做的是活跃变量分析或活性分析(liveness
analysis)。活跃变量分析是确定哪些变量在程序点保持活跃的过程。结合控制流图,就是判断变量x在程序点p上的值是否会在流图中的某条从点p出发的路径中使用。如果是,就说x在p上活跃;否则就说x在p上是死的。活跃变量分析是一个后向数据流分析问题,因为当前变量x是否在未来的某个地方被用到,只能通过从后面节点的信息中获知。活跃变量分析的重要用途之一是为基本块进行存储器分配。一个值被计算保存到一个寄存器中后,很有可能在基本块中被使用。如果它在基本块中是死的,就不必在结尾处保存这个值。另外在所有寄存器被占用时,如果还需申请可用寄存器,应该考虑使用一个存储了已死亡的值的寄存器,因为该值无需保存到内存。
根据如下后向数据流方程对控制流图做活跃变量分析:
IN[B] = GEN[B] ∪(OUT[B]-KILL[B])
OUT[B] = ∪IN[S] , S∈Succ(B)下图是if (e > 0)分支的活跃变量分析过程:
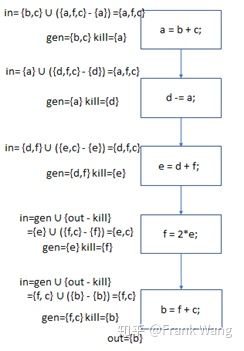
用类似的方法可以得到整个流图的活跃变量分析结果如下:
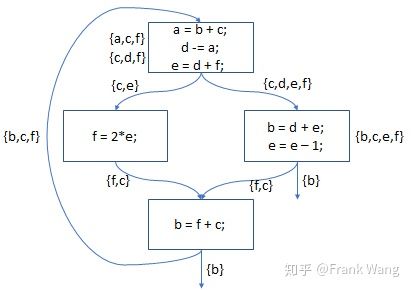
寄存器干涉图(RIG,Register Interference Graph)是一种无向图,用于显示在特定程序点哪些变量是活跃的,哪些寄存器在分配时会互相冲突。如果在程序点P存在两个变量a和b同时活跃,那么就称变量a和b在程序点P互相干涉。这时,变量a和b应分配不同寄存器。换言之,如果在寄存器干涉图上,两个节点之间没有边相连,则可以分配到同一寄存器。寄存器干涉图反映了对应流图的寄存器分配需求,活跃变量分析结果反应了哪些变量之间是互相冲突的,如,“f=2*e;”和“b=f+c;”之间的活跃变量是{f,c}。这说明f,c在这个程序点同时活跃,在它们对应的节点之间应该有边相连,且不能分配到同一寄存器。
根据如下构造干涉图的步骤,可以得到上例对应干涉图:
为每个变量添加一个节点;
检查变量之间的干涉。如果存在干涉,增加一条边;
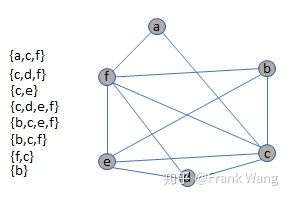
图着色过程可参考本文前述内容,此处不再赘述。图着色结果如下图:
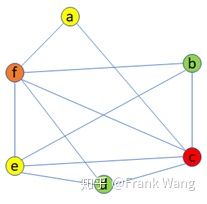
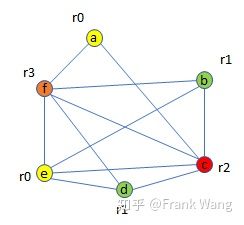
基于着色图分配寄存器的过程就是将不同颜色对应不同物理寄存器,颜色数量k对应物理寄存器数量。在本例中,通过图着色方法可以为六个变量(a-f)分配四个寄存器(r0-r3)而不产生冲突,如下图所示。当然,寄存器分配比较复杂,不仅仅是图着色的问题。比如,当物理寄存器数目不足以分配给所有变量时,就必须将某些变量溢出到内存中,即spill。最小化溢出代价的问题,也是一个NP-complete问题。
来源: zhuanlan.zhihu.com/p/55287942
作者: 汪岩